快速排序

发表于 | 分类于 | |
字数统计: 924 | 阅读时长 ≈ 4

引论

人如其名，快速排序之所以称之为快速排序就是因为在实践中，这个算法是最快的排序算法。它的平均运行时间为O(NlogN)。最坏的时间复杂度为O(N^2)。虽然像堆排序，归并排序的时间复杂度比较低，但是他们的实际运行时间并不比快速排序快，反而由于有一些拷贝的进程，使运行时间变得很慢。快速排序也是一种divide-and-conquer策略。

快速排序基本步骤：

  • 如果数据集S中的元素个数为0或1，则返回。

  • 选取S中的一个元素v，我们称这个元素v为pivot。

  • 把S-{v}分成两部分S1 = {x<=v} ，S2 = {x>=v}。

  • 返回quicksort(S1) ， v， quicksort(S2)。

quickSort

pivot的选择

pivot的选择是一个很大的问题。因为pivot直接影响到分开的两组数据的个数，而如果这两组数据是不均衡的，则会严重影响到算法的运行速度。举个例子来说，如果每次选择的pivot 都是最大值的话，那么这个快速排序算法相当于插入排序

pivot的选择有以下几种

  • 选取第一个值。这种算法适用于随机分布的数据。如果是一个有序的序列，那么这种选取方式就是一个灾难啊，将会不断的递归，也没有什么本质的提高

  • 随机选取一个值。这种方法也是看运气，如果选择了一个好的值就没有问题。但是如果选的值比较差，就会比较糟糕

  • 随机选取3个值，取中间值。这种方法对差值的风险抵抗能力比较强。一种常用的方法是选择数据的第一个值，中间的值，最后一个值。然后取这3个值得中间值。

代码片段

1
2
3
4
5
6
7
8
9
10
11
12
ElementType Median3(ElementType A[], int Left, int Right)
{
	int Center = (Left  + Right)/2;
	if(A[Left]>A[Center])
		Swap(&A[Left],&A[Center]);
	if(A[Left]>A[Right])
		Swap(&A[Left],&A[Right]);
	if(A[Center]>A[Right])
		Swap(&A[Center],&A[Right]);
	Swap(&A[Center],&A[Right-1]);
	return A[Right-1];
}

算法描述

这里，我们通过一个例子说明一下快速排序算法。

待排序数据为（8,34,51,21,18,64,26,32）首先利用上面的方法找到pivot为21，然后把pivot与A[N-1]=26交换位置。然后设定两个游标i，j。i向右滑动直到遇到大于pivot的值处停止，j向左滑动直到遇到小于pivot的值处停止，然后交换i，j对应的元素，然后继续上面的步骤知道i>j，然后交换i与pivot对应的元素。这样就把待排序数据集分成了两部分，然后递归调用上面的算法，最终得到排好序的数据。这里可能会有一个问题就是相等的元素，这将是一个特殊情形，例如数据中有几个值与pivot相等，那么当游标运动到了这几个位置时应该怎么办呢？游标继续向前走，越过这些值。

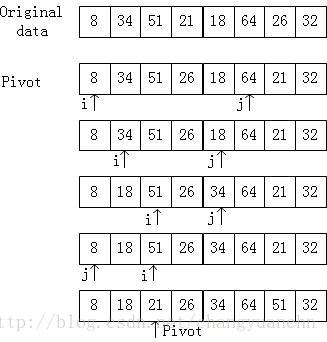
quickSort1

代码描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#define Cutoff (3)
void Qsort(ElementType A[], int Left, int Right)
{
	int i,j;
	ElementType pivot;
	if(Left + Cutoff <= Right)
	{
		pivot = Median3(A,Left,Right);
		i=Left;j=Right-2;
		for(::)
		{
			while(A[++i]<pivot){}
			while(A[--j]>pivot){}
			if(i<j)
				Swap(&A[i],&A[j])
			else
				break;
		}
		Swap(&A[i],&A[Right-2]);
		Qsort(A,Left,i-1);
		Qsort(A,i+1,Right);
	}
	else
		InsertionSort(A+Left,Right-Left+1);
}
 
 
void QuickSort(ElementType A[], int N)
{
	Qsort(A,0,N-1);
}

时间复杂度

$ O（NlogN）$

显示 Gitment 评论