引言
前面介绍了很多的排序算法,他们都是基于比较的思想的排序算法。基于比较的排序算法的理论的时间复杂度下限为$O(NlogN)$。
计数排序是一种非基于比较的排序算法,对一定范围内的整数排序时,它的复杂度为$Ο(n+k)$(其中$k$是整数的范围)。当然这是空间换时间得到的。
算法思想
计数排序的算法思想非常简单。
对于整数的排序来说,我们可以直接用数组的下标(数组的大小为待排序数据的最大最小值确定)来表示整数,进而可以直接统计每个整数的个数,进而实现排序的过程,如下图所示:

这样我们只需要按照顺序与次数输出下标的值即可完成排序。这就是最简单的计数排序的算法。
计数算法的变种
对于简单的整数排序,上面的排序算法没有问题,但是如果是下面的场景,就搞不定了。
假设有如下的排序场景,给定学生的课程表,要求成绩按照从低到高排序。如果成绩相同,则按原表顺序。
那么如果我们按照基础的计数排序就完蛋了,我们没有办法确定是小红排在前还是小绿排在前。


为了解决这个问题,我们将计数数组做一个变形,也就是统计数组从第二个元素开始,每一个元素都加上前面所有元素之和。

这样有什么好处呢?
这样我们按照原始数据的尾端开始遍历,就可以一步一步的找到他们排序后的位置
对于第一个0,我们根据数组的下标0找到他的位置应该是1。那么我们就可以把这个0放到最终的数组的1的位置,然后将计数数组的这个值减1。

对于遇到的第二个0,如上的操作。
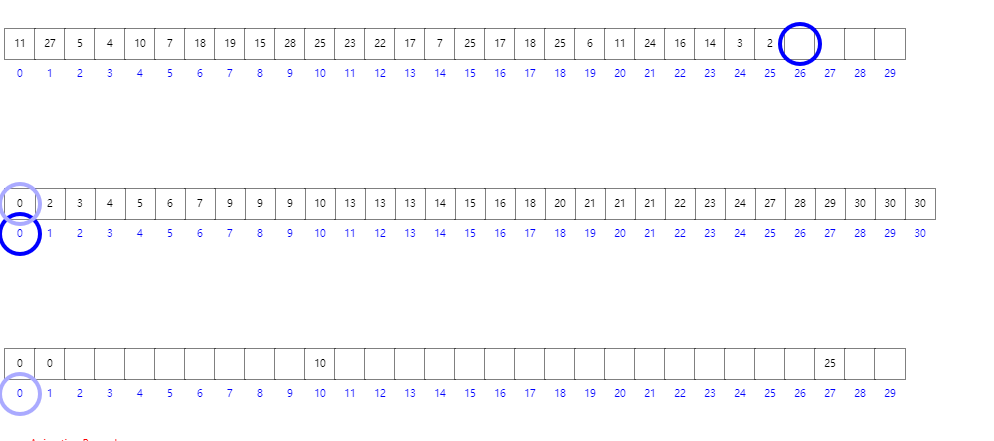
这样一步一步的对原始数据进行排序
这个改进的算法是属于稳定排序。
如果是小数,而不是整数该怎么办
这里可以用桶排序的方法,桶排序属于计数排序的推广算法