动态规划解决0/1背包问题

发表于 | 分类于 | |
字数统计: 1,836 | 阅读时长 ≈ 8

之前总结了利用穷举法，贪婪法解决0/1背包的方法，同时也通过Fibnacci介绍了动态规划，那么该如何来利用动态规划来解决0/1背包问题呢？

首先动态规划有两个条件;
如果可以把局部子问题的解结合起来得到全局最优解，那这个问题就具备最优子结构
如果计算最优解时需要处理很多相同的问题，那么这个问题就具备重复子问题

从这两点看，0/1背包问题跟动态规划没有半毛钱的关系啊。那这两者又是怎么联系起来的呢？我们通过二叉树将两者联系起来。

二叉树是一种树，每个跟节点至多有两个子节点。

我们可以将0/1背包问题通过二叉树来表示：

[0-1背包问题] 有一个背包，背包容量是M=150kg。有7个物品，物品不可以分割成任意大小。（这句很重要）
要求尽可能让装入背包中的物品总价值最大，但不能超过总容量。
物品 A B C D E F G
重量 35kg 30kg 6kg 50kg 40kg 10kg 25kg
价值 10 40 30 50 35 40 30

我们可以用下面的二叉树来表示问题的所有的解空间。

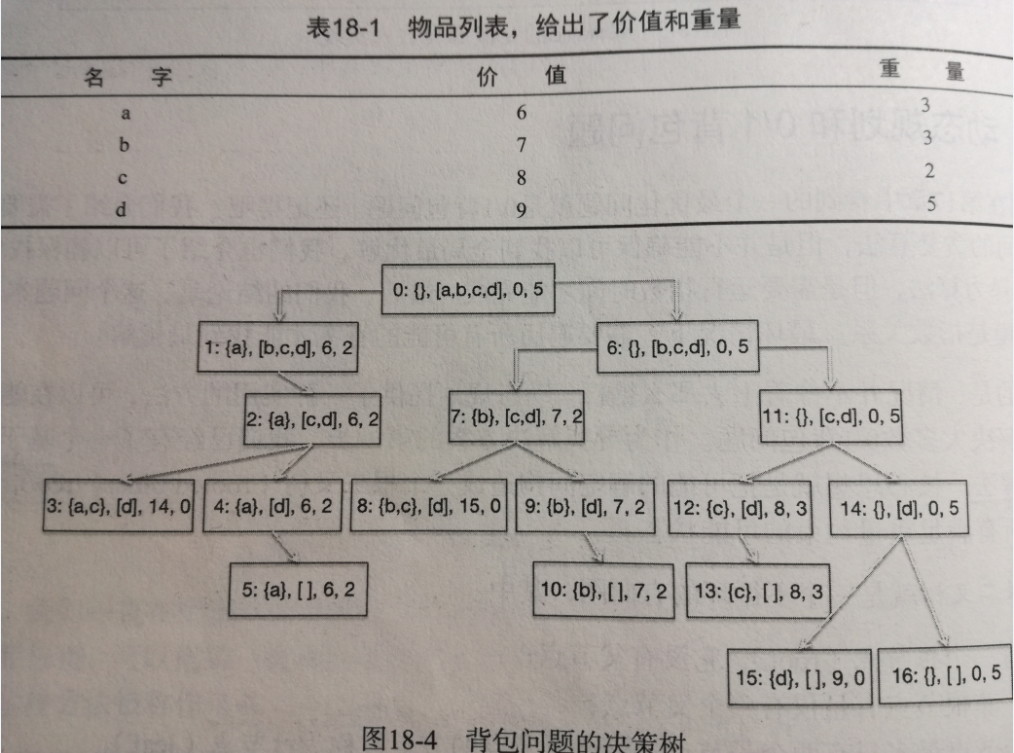
借个图，实在是不想画了
借个图，实在是不想画了，见谅

每个节点由四部分组成：

第一个集合表示：已经拿到背包里的物品
第二个集合表示：还没有决定要拿走的物品
第三个值表示：当前背包里的物品总价值
第四个值表示：背包剩余的重量

我们按照如下的策略进行生长

左子树表示：拿到了第二个集合中的第一个物品，右子树表示放弃掉第二个集合中的第一个物品

那么由着这个树一直生长下去，我们可以得到最终问题的解空间。

很明显这是一个可以用递归解决的问题。

那么下面就首先用递归的算法先来解决这个问题

对于递归来说要有一个边界条件，那么这里的边界条件有两个，一个是第二个集合为空（意味着全部拿走），另一个是第四个值为0（意味着背包已经装满了），而他们就是叶子节点，因为树的遍历或者说是递归只能是到达叶子节点就结束了。

普通递归方法求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# item have three attribute: name,weight,value
class Item(object):
    def __init__(self,n,v,w):
        self.name=n
        self.weight=float(w)
        self.value=float(v)
        
    def getName(self):
        return self.name
    
    def getValue(self):
        return self.value
    
    def getWeight(self):
        return self.weight
    
    def __str__(self):
        result = ' < '+self.name+' , '+str(self.value)+' , '+str(self.weight) + '>'
        return result
    


def maxValue(oraSet,leftRoom):
    # leaf 
    if oraSet == [] or leftRoom == 0:
        return (0,())
    # only right tree
    elif oraSet[0].getWeight() > leftRoom:
        result = maxValue(oraSet[1:],leftRoom)
    # select the best from the left and right
    else:
        # left tree, means we select nextItem(the first value of the remains)
        nextItem = oraSet[0]
        leftVal, leftToken = maxValue(oraSet[1:], leftRoom - nextItem.getWeight())
        leftVal +=nextItem.getValue()
        
        # right tree,means we do not select nextItem
        rightVal,rightToken = maxValue(oraSet[1:],leftRoom)
        
        if leftVal > rightVal:
            result = (leftVal,leftToken+(nextItem,))
        else:
            result = (rightVal,rightToken)
            
    return result


def buildItem():
    names=['A','B','C','D','E','F','G']
    vals = [35,30,6,50,40,10,25]
    weights=[10,40,30,50,35,40,30]
    Items=[]
    for i in range(len(names)):
        Items.append(Item(names[i],vals[i],weights[i]))
    return Items

def testCode():
    value,token = maxValue(buildItem(), 150)
    for item in token:
        print item
    print "Total value of tokens is ", value
    
testCode()
        
 < E , 40.0 , 35.0>
 < D , 50.0 , 50.0>
 < B , 30.0 , 40.0>
 < A , 35.0 , 10.0>
Total value of tokens is  155.0
time consumption is: 0.000482480256484

动态规划解法：

要想用动态规划，首先要满足两个条件：重复子问题 和 最优子结构
每个父节点会组合子节点的解来得到这个父节点为跟的子树的最优解，所以存在最优子结构。
同一层的每个节点剩余的可选物品集合都是一样的，所以具有重复子问题
因此可以利用动态规划来解决问题。

动态规划的核心就是提供了一个memory，能够缓存已经计算过的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# item have three attribute: name,weight,value
import time 
class Item(object):
    def __init__(self,n,v,w):
        self.name=n
        self.weight=float(w)
        self.value=float(v)
        
    def getName(self):
        return self.name
    
    def getValue(self):
        return self.value
    
    def getWeight(self):
        return self.weight
    
    def __str__(self):
        result = ' < '+self.name+' , '+str(self.value)+' , '+str(self.weight) + '>'
        return result
    

def fastMaxVal(oraSet,leftRoom,memo={}):
    if (len(oraSet),leftRoom) in memo:
        result = memo[(len(oraSet),leftRoom)]
    elif oraSet == [] or leftRoom == 0:
        result = (0,())
    elif oraSet[0].getWeight()>leftRoom:
        result = fastMaxVal(oraSet[1:],leftRoom,memo)
    else:
        nextItem = oraSet[0]
        
        leftValue,leftToken = fastMaxVal(oraSet[1:],leftRoom - nextItem.getWeight(),memo)
        leftValue +=nextItem.getValue()
        
        rightValue,rightToken = fastMaxVal(oraSet[1:],leftRoom,memo)
        
        if leftValue >rightValue:
            result = (leftValue,leftToken+(nextItem,))
        else:
            result = (rightValue,rightToken)
        
    memo[(len(oraSet),leftRoom)] = result
        
    return result



def buildItem():
    names=['A','B','C','D','E','F','G']
    vals = [35,30,6,50,40,10,25]
    weights=[10,40,30,50,35,40,30]
    Items=[]
    for i in range(len(names)):
        Items.append(Item(names[i],vals[i],weights[i]))
    return Items

def testCode():
    value,token = fastMaxVal(buildItem(), 150)
    for item in token:
        print item
    print "Total value of tokens is ", value

start=time.clock()
testCode()
end = time.clock()
print "time consumption is:", end-start
1
2
3
4
5
6
 < E , 40.0 , 35.0>
 < D , 50.0 , 50.0>
 < B , 30.0 , 40.0>
 < A , 35.0 , 10.0>
Total value of tokens is  155.0
time consumption is: 0.000385599247536

可以看出相较于最基本的递归方法，动态规划还是更快一些的，当然这里快的不明显，因为数据量表小，但是当数据量比较大时，这个时间的节省就比较可观了。

思考：

1） 动态规划为什么会快？

因为这里不需要调用函数计算重复子问题，那么一定就是快很多么？不一定，这取决于重复子问题的多少。0/1背包问题当数据量大时，他的时间节省比较多的原因在与我们设计的重复子问题比较好，因为对于物品的多种组合来说，他们的剩余空间的一致的概率比较大，多以告知重复子问题会比较多。

2）动态规划的核心：

核心在于memory的设计，这里我们利用了memo[(len(oraSet),leftRoom)]中的(len(oraSet),leftRoom)字典作为键，为什么可以利用len(oraSet)而不是oraSet呢（当然oraSet也是可以的）？这是因为对于每一层的子节点来说，剩余物品的个数都是一致的，这个个数可以区分重复子问题。而动态规划相较于普通的递归算法，主要的就是增加了memory

3）如何设计动态规划算法：

首先看问题是否满足动态规划的两个条件：重复子问题，最优子结构；然后首先利用递归算法解决问题，设计memory，然后修改递归算法的实现，加入memory，最终实现动态规划的算法。

显示 Gitment 评论