分治算法

发表于 | 分类于 | |
字数统计: 1,034 | 阅读时长 ≈ 4

分治算法的名字是divide-and-conquer, 从名字上看一目了然，就是先把一个问题divide成为几个子问题，然后分别解决各个子问题。兵法有云：分而治之，各个击破。

英文释义

divide the problem instance, solve subproblems recursively, combine the results, and thereby conquer the problem

算法内涵

分治算法就是把一个困难的问题分解为一系列的子问题，这些子问题具有如下的特点：
1） 子问题比原问题更新解决
2） 子问题的解可以合并为原问题的解

典型的应用包括回文以及二分查找等。

算法举例

回文

这里的回文是指资格字符串，它从头到尾读与从尾到头读的内容是一致的，比如说doggod,无论从左到右耗时从右到左都是一样的。

1
2
3
4
5
6
7
8
9
def isPal(s):
    if len(s) <= 1:
        return True
    else:
        return s[0]==s[-1] and isPal(s[1:-1])
    
s = 'doggod'
result = isPal(s)
print result

可以看出算法就是利用递归不断的处理更小的子问题。

二分查找

二分查找也是典型的分治算法的有应用。二分查找需要一个默认的前提，那就是查找的数列是有序的。
二分查找的思路比较简单：
1） 选择一个标志i将集合分为二个子集合
2） 判断标志L(i)是否能与要查找的值des相等，相等则直接返回
3） 否则判断L(i)与des的大小
4） 基于判断的结果决定下步是向左查找还是向右查找
5） 递归记性上面的步骤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def binarySearch(L,e,low,high):
    if high == low:
        return L[low] == e 
    mid = (low+high)//2
    if L[mid]==e:
        return True
    elif L[mid]>e:
        if low == mid:
            return False
        else:
            return binarySearch(L,e,low, mid-1)
    else:
        return binarySearch(L,e,mid+1,high)

def search(L,e):
    result = binarySearch(L,e,0,len(L)-1)
    print result   
    
L = range(10);
e = 7

search(L,e)

最近点问题

假设在坐标平面上分布了一系列的点，那么问题是求取这些点两两之间的最短距离。

最naive的做法当然是穷举法，计算所有的两两点间的距离，然后取最小值。穷举法对于小样本总是不错的。但是对于大样本来说，就不是那么合适了，这里我们用divide-and-conquer算法来解决这一问题。

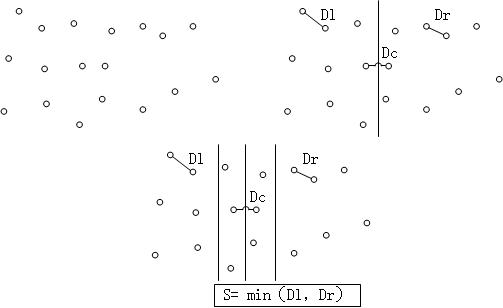
divideConquer

首先对于所有的点，按照x坐标将其分为两部分，这就是divide，那么最短距离就是左边部分中的最短距离Dl，右边部分的最短距离Dr，以及左右部分之间的距离Dc。对于Dl以及Dr，可以递归的计算得到，这就是conquer。那么唯一的问题就是Dc。我们知道如果最短距离是Dc的话，那么Dc<=min（Dl，Dr）。因此我们只需要计算距离divide分割线S = min（Dl，Dr）的点就可以了。进一步我们可以看到对于每个在2S区域内的点，只需要计算y坐标距离这一点不大于S的点就可以，这样可以进一步简化运算量。

1
2
3
4
5
6
7
for(i=0;i<NumPointsInStrip;i++)
	for(j=i+1;j<NumPointsInStrip;j++)
		if(Pi and Pj coordinates differ by more than S)
			break;
		else
			if(Dist(Pi,Pj)<S)
				S = Dist(Pi,Pj);

总结

分治算法的一个核心在于子问题的规模大小是否接近，如果接近则算法效率较高。

分治算法和动态规划都是解决子问题，然后对解进行合并；但是分治算法是寻找远小于原问题的子问题（因为对于计算机来说计算小数据的问题还是很快的），同时分治算法的效率并不一定好，而动态规划的效率取决于子问题的个数的多少，子问题的个数远小于子问题的总数的情况下（也就是重复子问题多），算法才会很高效。

显示 Gitment 评论