logistic回归

引言

logistic回归是一种很早期的回归模型，属于广义的线性回归，用于数据挖掘，经济预测等多种场景。本章我们首先引入线性回归模型，然后给出逻辑回归的定义，以及二次逻辑回归，同时给出logistic回归的参数训练方法，最后给出logistic回归于神经网络的关系

线性回归

所谓的线性回归，其实就是用下面的公式来对数据进行分类或者回归的模型。

$$z = w_0+w_1x_1+w_2x_2+...+w_nx_n = wx$$

图示如下所示：

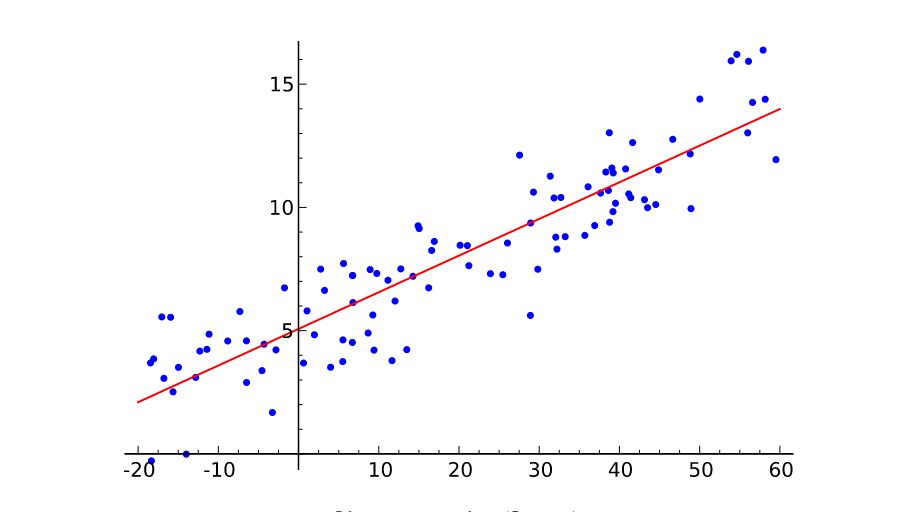
本质上讲就是利用线性方程来划分分类平面的模型

二项logistic回归

二项logistic回归就是如下的条件概率分布

$$P(Y=1|x) = \frac{e^{wx}}{1 + e^{wx}}$$ $$P(Y=0|x) = \frac{1}{1 + e^{wx}}$$

其中$wx = w_0+w_1x_1+w_2x_2+...+w_nx_n$ 就是上面的线性分类器

因此二项logistic回归就是利用logistic函数，根据输出，将目标分成两类。logistic回归是一种概率化的模型。训练二项logistic回归，本质上就是通过给定的输入$x$训练模型参数$w$。后面我们会讲解如何训练模型参数，下面我们先介绍一下logistic分布。

logistic分布

假设$X$为连续随机变量，$X$服从logistic分布是指$X$具有下面的分布函数和密度函数：

$$F(X) = P(X \leq x) = \frac{1}{1 + e^{\frac {-(x- \mu)}{\gamma}}}$$ $$f(X) = F'( x) = \frac{e^{\frac {-(x- \mu)}{\gamma}}}{\gamma(1 + e^{\frac {-(x- \mu)}{\gamma}})^2}$$

看着函数比较复杂，其实画出其图像就简单了

其实概率密度函数是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分

因此通过分布函数我们可以推导出上面的二项logistic回归，同样的也可以推导出多项logistic回归方程，如下所示，

多项logistic回归

多项logistic回归有下面的模型

$$P(Y=k |x) = \frac{e^{w_k x}}{1 + \sum^{K-1}_{k=1}{e^{wx}}} \qquad 其中 k=1,2,...,K-1$$ $$P(Y=K |x) = \frac{1}{1 + \sum^{K-1}_{k=1}{e^{wx}}}$$

参数学习

下面我们已二项logistic回归为例子，用极大似然估计来推导logistic回归的参数学习。

另：

$$P(Y=1|x,\theta) = \frac{e^{\theta x}}{1 + e^{\theta x}} =h_{\theta}(x)$$ $$P(Y=0|x,\theta) = \frac{1}{1 + e^{\theta x}} =1-h_{\theta}(x)$$

则条件概率分布:

$$P(y|x; \theta) = (h_{\theta})^y(1-h_{\theta})^{1-y}$$

假设用于训练的m个样本独立，所以样本的条件概率分布的似然函数如下所示：

$$L(\theta) = \prod_{i=1}^{m} P(y^i|x^i; \theta) = (h_{\theta})^{y_i}(1-h_{\theta})^{1-y_i}$$

我们的目标就是最大化这个函数$L(\theta)$

将上面的等式取对数有

$$l(\theta) = log(\prod_{i=1}^{m} P(y^i|x^i; \theta) )= \sum_{i=1}^{m} (log( (h_{\theta})^{y_i}) +log( (1-h_{\theta})^{1-y_i}) )$$ $$l(\theta) = \sum_{i=1}^{m} ({y_i}log (h_{\theta}) +{(1-y_i)} log(1-h_{\theta}) )$$

因此目标转变为了最大化函数$l(\theta)$，也可以转换为最小化下面的函数

$$-l(\theta) = \frac{1}{m}\sum_{i=1}^{m} ({y_i}log (h_{\theta}) +{(1-y_i)} log(1-h_{\theta}) )$$

这个函数好熟悉啊，这个不就是之前在神经网络之代价函数的选择这一章节引入的交叉熵代价函数么，好巧啊，那么我们也可以用梯度下降算法来学习参数了啊。

logistic回归与神经网络的关系

我们将神经网络进行简化，去掉隐藏层，输出层为1个神经元，神经元选择为logistic神经元，我们发现这是的神经网络就是logistic回归。

只不过神经网络的输出为$\sigma = \frac{1}{1+e^{-z}}$， 这正好对应着二项logistic中的$P(Y=0|x)$

因此我们可以按照神经网络中的梯度下降算法来更新logistic回归模型里面的参数。

后记

logistic回归模型更新权重的方法还有迭代尺度法和拟牛顿法，这个后面有时间在更新。