决策树

引言

决策树是一种树模型，本质上讲就是利用特征对空间进行划分的一种方法。在计算机的数据结构里面我们有二叉树等等模型，在思想上，决策树与他们是一样的。决策树是一种最简单的机器学习算法，甚至某种程度上把它当做机器学习算法有点别扭。对于决策树算法来说，主要包括两点：

• 以什么样的规则选择根节点
• 剪枝防止过拟合

常见的决策树算法有ID3，C4.5，CART等算法，我们下面来一一介绍

决策树模型

决策树是一种利用实例特征对空间进行划分的模型，由节点和有向边组成。内部节点表示属性或者特征，叶子节点表示类别。下图就是一个典型的决策树的例子。

对于常规的机器学习问题，给定了数据集，构造决策树模型，那么首先第一个问题就是选择哪个特征作为根节点。业界提出了信息增益的概念，利用信息增益我们就可以计算出什么特征作为根节点最优了。

在给出信息增益的计算方式之前，首先需要介绍一下信息熵的概念

信息熵

初中物理我们学过熵，熵实际上是物质无序状态的一种度量。

信息熵是大神Shanon提出的概念，用于表示信息多少的概念。设$X$是一个离散随机变量，其概率分布为$P(X = x_i) = p_i \quad i=1,...,n$,则我们定义随机变量$X$的熵为：

$$H(X) = - \sum_{i=1}^{n} p_i logp_i$$

我们看一个二分类问题的熵的图像：

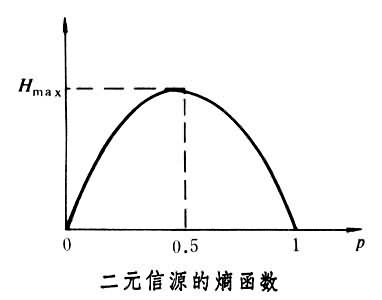
我们可以看到当$p=0.5$的时候，熵最大，这也就意味着越无序，越没有确定性的时候，熵越大。在信息论里，不确定性越高，信息越多。

有了熵的定义，下面我们来引入条件熵的概念：

设随机变量$(X,Y)$，其概率分布为$P(X = x_i,Y=y_j) = p_{ij} \quad i=1,...,n, j=1,...,m$,则我们定义给定随机变量$X$的条件下，随机变量$Y$的条件熵为：

$$H(Y|X) = \sum_{i=1}^{n} p_i H(Y|X=x_i)$$

有了熵和条件熵，我们就可以引入信息增益的概念

信息增益

给定特征A对训练集D的信息增益$g(D,A)$ 可以简单的用下面的公式计算：

$$g(D,A) = H(D) - H(D|A)$$

$ H(D) $ 表示数据集D的不确定性，$H(D|A)$ 表示给定特征A的情况下，数据集D的不确定性。他们的差就表示给定了特征A的场景下，数据集D的不确定性减少的程度。程度越大，说明特征A越能有效的对数据进行分类，因此可以利用信息增益来选择递归决策树的根节点

如何计算信息增益

假设数据集为$D$ ,$|D|$ 为数据集的容量，数据集有$K$个类$C_k$, $|C_k|$ 为$C_k$的样本个数，$\sum^K_{k=1} |C_k| = |D|$。设特征$A$ 将样本D划分为$n$个子集$D_1,...,D_n$ ，子集$D_i$ 中属于类$C_k$的集合为$D_{ik}$.因此信息增益可以有下面的式子计算得到：

$$H(D) = - \sum^K_{k=1} \frac {|C_k|}{|D|} log \frac {|C_k}{|D|}$$ $$H(D|A) = \sum^n_{i=1} \frac {|D_i|}{|D|}H(D_i) = \sum^n_{i=1} \frac {|D_i|}{|D|} \sum_{k=1}^{K} \frac {|D_{ik}|}{|D_i|} log \frac {|D_{ik}|}{|D_i|}$$

因此信息增益为：

$$g(D,A) = H(D) - H(D|A)$$

信息增益比

由于以信息增益作为划分数据集的特征，存在偏向于选择取值较多的特征，因此引入了信息增益比来选择特征。

信息增益比为：

$$g_R(D,A) = \frac {g(D,A)}{H_A(D)}$$

其中${g(D,A)}$为信息增益，${H_A(D)}$为数据集关于特征$A$的熵,其计算公式如下：

$$H_A(D) = - \sum^n_{i=1} \frac {|D_i|}{|D|} log \frac {|D_i}{|D|}$$

其中$n$为特征$A$取值的个数

ID3算法

其实ID3算法很简单，就是一句话，利用信息增益递归的选择根节点来分类数据直至所有的特征选择完毕

下面我们也给一下具体的算法吧

输入

• 训练数据集 $D = \left \{ (x_1,y_1),...,(x_N,y_N) \right \}$
• 阈值$\varepsilon$
• 特征$A$

算法流程

• 若 $D$中所有的实例都属于同一类$C_k$，则$T$为单节点树，将类别$C_k$作为类标记，返回$T$
• 若$A = \varnothing$，则$T$为单节点树，将 $D$中实例数目最多的类别$C_k$作为类标记，返回$T$
• 否则，按照$g(D,A) = H(D) - H(D|A)$计算$A$中各特征对$D$的信息增益，选择信息增益最大的特征$A_g$
• 如果$A_g$的信息增益小鱼阈值$\varepsilon$，则设置$T$为单节点树，将 $D$中实例数目最多的类别$C_k$作为类标记，返回$T$
• 否则，对$A_g$的每一个可能值$a_i$的，按照$A_g = a_i$将$D$分割为若干个非空子集$D_i$，将$D_i$中实例数最大的类作为标记，构建子节点，由节点及其子节点构成树$T$，返回$T$
• 对第$i$个子节点，以$D_i$为训练集，以$A - \left \{A_g \right \}$为特征集，递归调用上面的步骤，得到子树$T_i$,返回$T_i$

输出

• 决策树 $T$

C4.5算法

C4.5算法跟ID3的不同就在于C4.5算法利用了信息增益比来选择特征。因此具体算法流程跟上面是一样的，因此这里不再阐述。

剪枝

上面我们引入了C4.5算法和ID3算法，算法通过规则选择根节点，然后依次递归对每一个特征进行遍历构建决策树。但是这样有一个问题啊，那就是决策树很容易过分的适应训练数据，进而实现过拟合，因此引入剪枝来消除决策树的过拟合问题。

剪枝最简单的算法如下

输入

• 决策树T

过程

• 对给定的决策树从最底层的非叶节点开始剪枝，每次剪一个非叶节点
• 将剪枝的非叶节点替换为叶节点，利用投票决定其类别
• 依次剪枝，生成剪枝树的集合$\left \{T,T_1,T_2,... \right \}$
• 利用cross-validation算法选择效果最好的子树$T_{best}$

输出

• 剪枝后的决策树$T_{best}$

CART算法

$CART$算法全称为$( classification \quad and \quad regression \quad tree)$，是一种广泛应用的决策树方法。$CART$算法由特征选择，树生成和树剪枝构成。$CART$算法关于决策树的生成就是递归的构建二叉决策树的过程,根据内部节点的特征的取值为“是”或者“否”，来划分两个分支。由她的名字我们也可以看出，$CART$包括回归树和分类树两种，对回归利用平方误差最小化准则，对分类树利用基尼系数最小化准则。下面我们来分别引入这两种树。

回归树

对于回归树来说,它学习到的模型，本质上来讲就是对输入空间进行划分，假设划分为$R_1,...,R_M$，那么输入空间划分后，就可以利用平方误差准则来训练得到空间的输出$c_m$,因此我们的回归树模型就如下所示：

$$f(x) = \sum_{m=1}^{M} c_mI(x \in R_m)$$

根据平方误差准则，求训练样本的最大似然估计，有：

$$\hat{c_m} = ave(y_i | x_i \in R_m)$$

那么问题就转化为了如何有效的对空间进行划分，如果空间划分完毕了，$\hat{c_m}$也就能够计算出来了（$\hat{c_m}$就是空间$R_m$内样本的标签的均值）。

那么给定训练数据集 $D = \left \{ (x_1,y_1),...,(x_N,y_N) \right \}$，如何对输入空间进行划分呢？这里我们采用启发式的算法。

假设我们选择第$j$个变量$x_j$和她的值$s$最为切分变量和切分点，那么可以得到两个区域

$$R_1(j,s) = \left \{ x|x_j \leq s \right \}$$ $$R_2(j,s) = \left \{ x|x_j > s \right \}$$

那么寻找最优的切分变量$j$和切分点$s$，就是求解

$$min_{j,s} [min_{c_1} \sum_{x_i \in R_1(j,s)} (y_i-c_1)^2 + min_{c_2} \sum_{x_i \in R_2(j,s)} (y_i-c_2)^2]$$

对固定输入的切分变量$j$，可以找到最优的切分点$s$

$$\hat{c_1} = ave(y_i|x_i \in R_1(j,s))$$ $$\hat{c_2} = ave(y_i|x_i \in R_2(j,s))$$

遍历所有的输入变量，找到最优的切分变量$j$，构成$(j,s)$将空间划分为两个区域。递归的重复上面的过程，直到满足停止条件。

回归树具体算法：

输入

• 样本集 $D = \left \{ (x_1,y_1),...,(x_N,y_N) \right \}$

算法流程

• 在训练样本的输入空间中，递归的将每个区域划分为两个子区域并决定每个子区域的输出值，构建二叉树。

• 1.选择最优的切分变量$j$和切分点$s$，求解$min_{j,s} [min_{c_1} \sum_{x_i \in R_1(j,s)} (y_i-c_1)^2 + min_{c_2} \sum_{x_i \in R_2(j,s)} (y_i-c_2)^2]$，遍历$j$，对固定的$j$扫描切分点$s$，得到是公式最小的值对$(j,s)$
• 2.对选定的值对值对$(j,s)$划分区域，并决定区域的输出值：$R_1(j,s) = \left \{ x|x_j \leq s \right \}$，$R_2(j,s) = \left \{ x|x_j > s \right \}$，$\hat{c_m} = ave(y_i | x_i \in R_m)$
• 3.继续对上面两个子区域调用步骤1，2，直至满足停止条件
• 4.将输入空间划分为$M$个区域$R_1,...,R_M$，生成决策树$f(x) = \sum_{m=1}^{M} c_mI(x \in R_m)$

输出

• 回归树 $f(x)$

分类树

对于分类树，我们采用基尼系数最小准则来确定最优的切分点

基尼系数

假设$K$类分类问题，样本点属于第$K$类的概率为$p_k$,则概率分布的基尼系数为：

$$Gini(p) = \sum_{k=1}^{K} p_k(1-p_k) = 1 - \sum_{k=1}^{K} p_k^2$$

给定样本$D$，其基尼系数为：

$$Gini(D) = 1 - \sum_{k=1}^{K} (\frac{|C_k|}{|D|})^2$$

其中$C_k$是$D$中属于第$k$类的样本的子集。

如果样本$D$根据特征$A$是否取某一可能值$a$被分割为$D_1,D_2$两部分，即：

$$D_1 = \left \{ (x,y) \in D| A(x) = a \right \} $$, $$D_2 = D - D_1$$

则在给定特征$A$的条件下，集合$D$的基尼系数定义为：

$$Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$$

分类树具体算法

输入

• 样本集 $D = \left \{ (x_1,y_1),...,(x_N,y_N) \right \}$
• 停止条件

算法流程

• 在训练样本的输入空间中，递归的对每个节点进行下面的操作，构建二叉树。

• 1.计算现有特征对数据集$D$的基尼系数，对每一个特征$A$，对其可能取值$a$，根据样本点对$A = a$的测试结果为“是”或者“否”将$D$分割为$D_1,D_2$两部分，利用$Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$计算$A = a$的基尼系数
• 2.对所有可能的特征$A$，以及他们的所有可能的切分点特征$a$中，选择基尼系数最小的特征及其对应的切分点为最优特征和最优切分点，生成两个子节点，将训练数据划分到两个子节点中。
• 3.继续递归调用步骤1，2，直至满足停止条件

输出

• 决策树 $f(x)$

CART剪枝

最简单的方式是预先预留数据作为验证集，对生成树从底部一步一步剪枝，得到子树序列（每一次剪枝就是将最底层的非叶节点变为叶节点，其类别利用投票法决定），利用验证集选择出效果最好的子树，剪枝完毕。