引言

双指针的算法并不是什么二分查找，回溯等那样的算法，它更像是一种奇巧淫技，通过一定的技巧和心计，能够在较低的时间复杂度内巧妙的完成一系列的遍历问题，下面我们就通过一些leetcode的习题来看下双指针的使用。

实际上在我们的基础数据结构中，只有两种，一种是数组，一种是链表，其他的像树，队列，堆等等，都可以用数组或者链表来实现。而数组也可以被看作是一种特殊结构的链表。因此实际上数据结构就只有一种，也就是链表。而链表的标准结构，就是有一个指向下一个节点的指针，通过这个递归的指针访问，我们就可以访问到所有的元素。

而双指针就是意味着我们将用两个指针来实现遍历。这两个指针一般是不同步的，有快有慢，要么是间隔一定距离后同步前进，要么是在两端向中心逼近，要么是各自指向各自的位置，然后进行融合。无外乎就这么几种场景，下面我们来分别总结分析下。

合并链表

这是最基础的形式，基本上不需要双指针的技巧，算是本能的场景

合并两个链表

如下的leetcode题目[合并两个有序链表(https://leetcode-cn.com/problems/merge-two-sorted-lists/)

我们首先创建一个dummy的头节点，然后比较两个链表，把较小的值依次链接到dummy节点上即可。这个题目比较简单，代码如下所示。

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        struct ListNode* dummy = new ListNode(-1);
        struct ListNode* p = dummy;
        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val <= list2->val) {
                p->next = list1;
                list1 = list1->next;
            } else {
                p->next = list2;
                list2 = list2->next;
            }
            p = p->next;
        }
        if (list1 == nullptr) {
            p->next = list2;
        }
        if (list2 == nullptr) {
            p->next = list1;
        }
        return dummy->next;
    }
};

另外多说一句，这个题目更加简洁的做法是直接用递归解决，不过这不是我们今天的主题。代码如下所示：

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (l1 == nullptr) {
            return l2;
        }
        if (l2 == nullptr) {
            return l1;
        }
        if (l1->val < l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        } else {
            l2->next = mergeTwoLists(l1, l2->next);
            return l2;
        }
        return l1;
    }
};

合并k个有序链表

如下的leetcode题目[合并k个有序链表(https://leetcode-cn.com/problems/merge-k-sorted-lists/)

这个题目是上面题目的扩展，

一个朴素的想法是，既然我们有了合并两个链表的经验，那么我们可以每次合并两个链表，直到把k个链表合并完毕。但是这样会花费大量的遍历时间，进行大量的重复遍历。
另一个朴素的做法是既然是k个链表，那么我们就k个指针，然后进行比较合并，但是这个也不是一个可执行的方案。因为这已经没有是事例编程了，没有任何的抽象了。
另一个朴素的做法是我们可以把k个链表的指针的值进行排序，然后依次链接到一起。

对与最后一种解决方案，我们需要一个数据结构来对其进行管理，显然最小堆是最合适的

class Comp{
    public:
    bool operator()(ListNode* a,ListNode* b){
        return a->val > b->val;
    }
};
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if (lists.size() == 0) return nullptr;
        ListNode* dummy = new ListNode(-1); // 创建一个dummy的节点
        ListNode* p = dummy;
        priority_queue<ListNode*,vector<ListNode*>,Comp> pQueue; // 创建最小堆
        for (auto list : lists) {
            if (list == nullptr) {
                continue;
            }
            pQueue.push(list);  // 将所有的链表的头节点push到最小堆中
        }
        while (!pQueue.empty()) {
            ListNode* node = pQueue.top(); // 取第一个元素，因为是最小堆，所以一定是最小的值
            pQueue.pop();
            p->next = node;
            if (node->next != nullptr) {
                pQueue.push(node->next); // 处理完这个最小值后，将其本身链表的下一个值push到最小堆中
            }
            p = p->next;
        }
        return dummy->next;
    }
};

单链表的倒数第K个节点

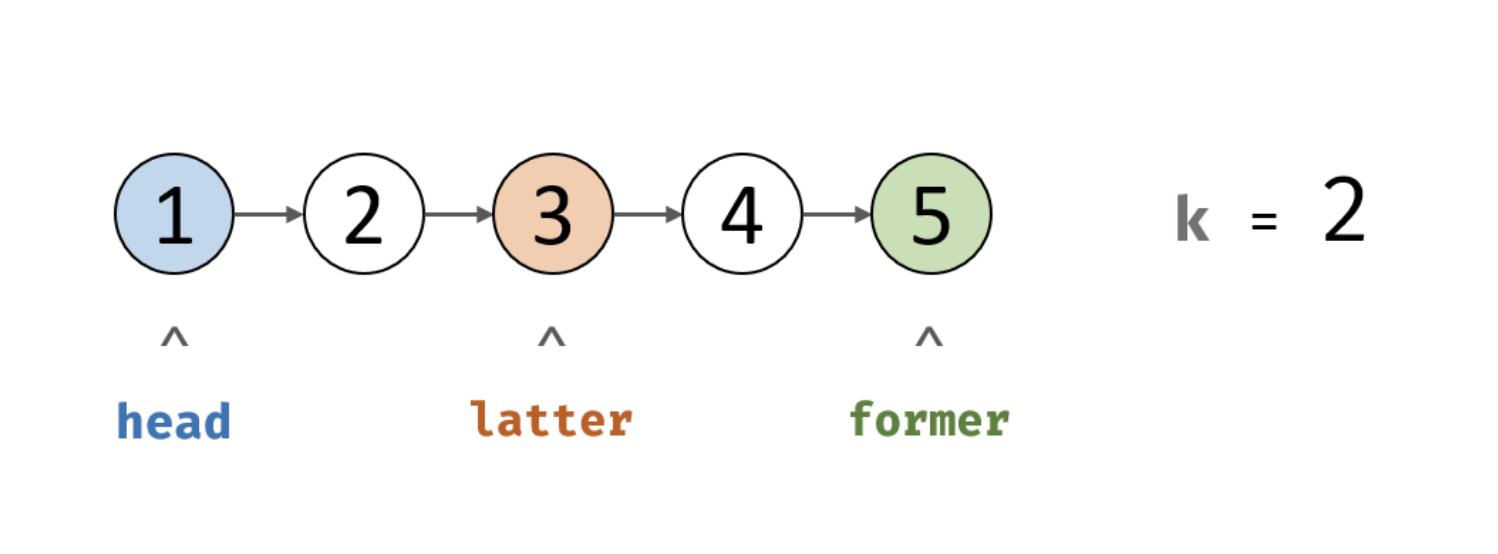
单向链表是只能正向遍历的，没法倒序遍历的。其次除非遍历一遍，否则我们是不知道链表的节点个数的，因此如果要求返回倒数的第k个节点，那么一个朴素的方法就是遍历两遍，第一遍遍历得到节点个数，第二次按照个数减去k的步骤走到指定的节点。那么能否只遍历一遍就得到结果呢？用双指针就可以解决了。

如下的leetcode题目[单链表的倒数第K个节点(https://leetcode-cn.com/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/)

我们可以指定两个指针，一个指针先走k步，然后他们同步走，这样当先走的指针到达终点时，慢的那个指针就正好指向了倒数第K个节点，如图所示：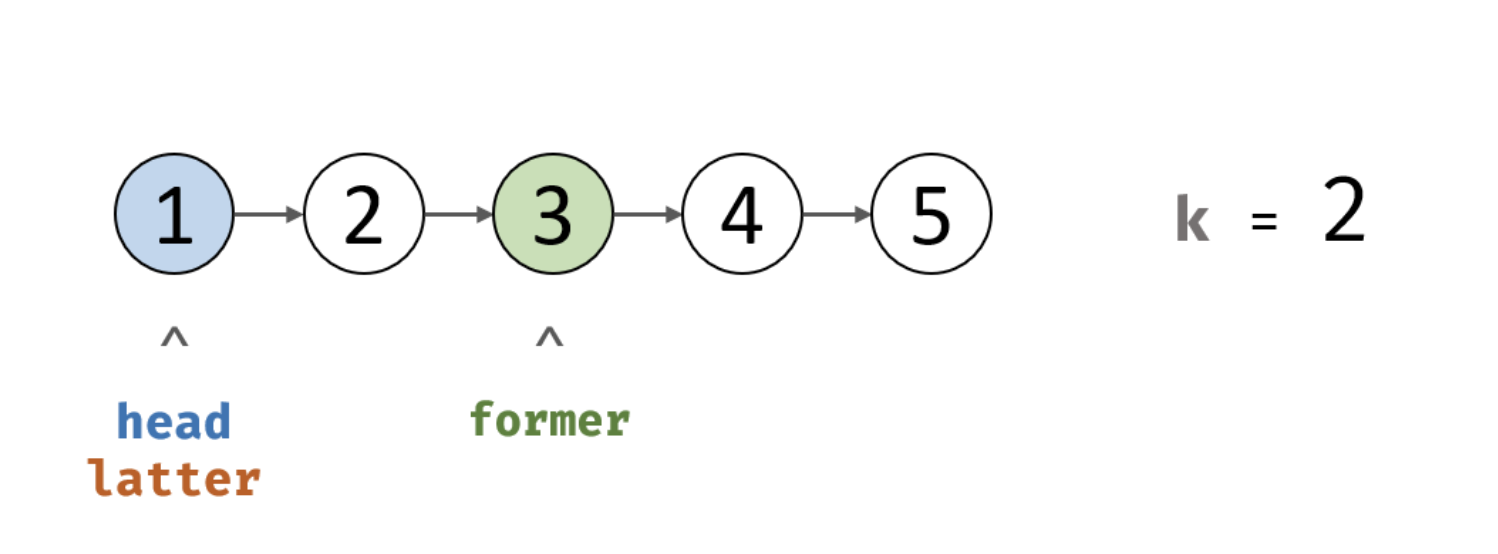

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        ListNode* fast = head;
        ListNode* slow = head;
        int i = 0;
        while (i++ < k ) {
            fast = fast->next;
        }
        while (fast != nullptr) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};

单向链表的中间结点

单向链表的中间结点
这个跟上面的很像，但是如果采用上面的思路，会有个问题，那就是我们没法确定先走多少步，这个得遍历完链表才行。如果遍历完链表，就没有必要用上面的方法了，直接走就行了。如果要遍历一次的话，可以每次让fast指针走两步，slow指针走一步，这样当fast指针走到终点的时候，slow也走到中点了。

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;
    }
};

判断链表是否有环

如判断链表是否有环此题所示

所谓的环形链表，如下所示。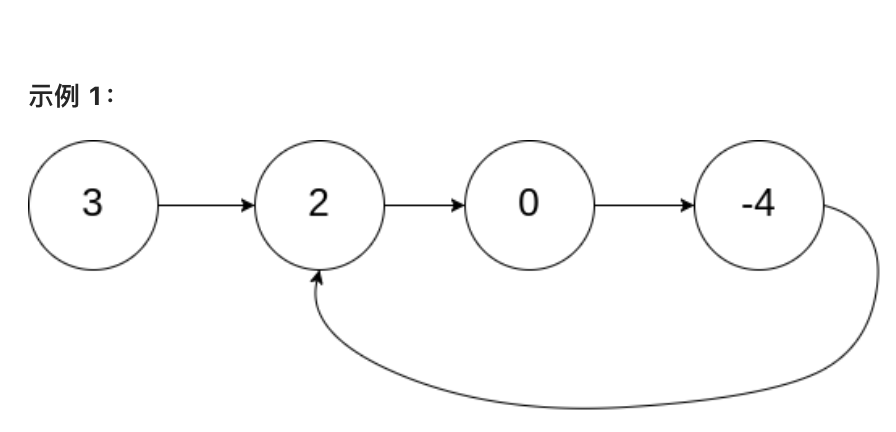

有环的话，实际上意味着我们永远也没有办法到达终点，也就是会一直转圈圈。就像我们在操场做圆形跑步，如果一个快，一个慢，那么无论从那个点开始，快的那个总是会在某一个追上慢的。因此用快慢指针就可以解决这个问题（这里速度是没有要求的，不过一般都是fast走两步，slow走一步），如果快慢指针有一个时刻指向了同一个节点，那么一定说明这个链表是环形链表。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                return true;
            }
        }
        return false;
    }
};

如果要返回开始入环的第一个节点呢？如返回环形链表的入环节点所示。

同样的我们首先要找到相遇的点，然后fast指针指向head节点，与slow相同的速度走，那么下次相遇的点，就是他们环的入环节点。原理如下：
第一次相遇的点，那么fast一定比slow多走了一圈，那么对于slow走了x+y，对于fast走了x+y+z+y。而fast的步数是slow的两倍，那么就有：
x + y + z + y == 2 *（x + y）因此有z = x；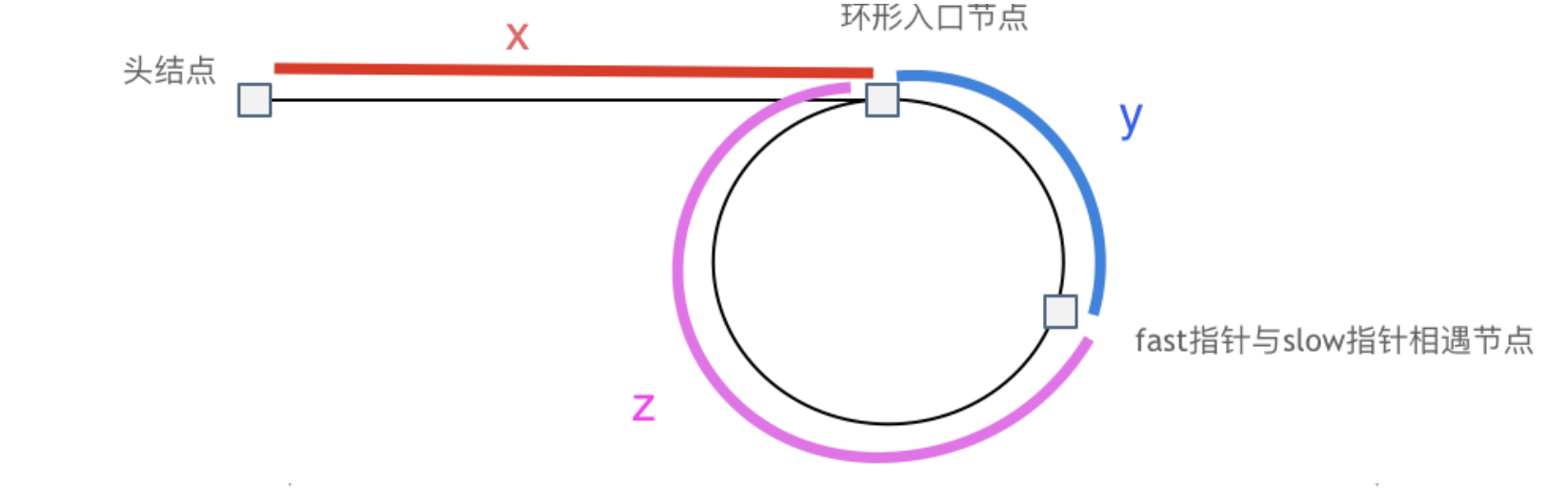

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                break;
            }
        }

        if (fast == nullptr || fast->next == nullptr) {
            return nullptr;
        }

        fast = head;
        while (fast != slow) {
            fast = fast->next;
            slow = slow->next;
        }
        return fast;
    }
};

判断链表是否相交

所谓的链表相交如下所示：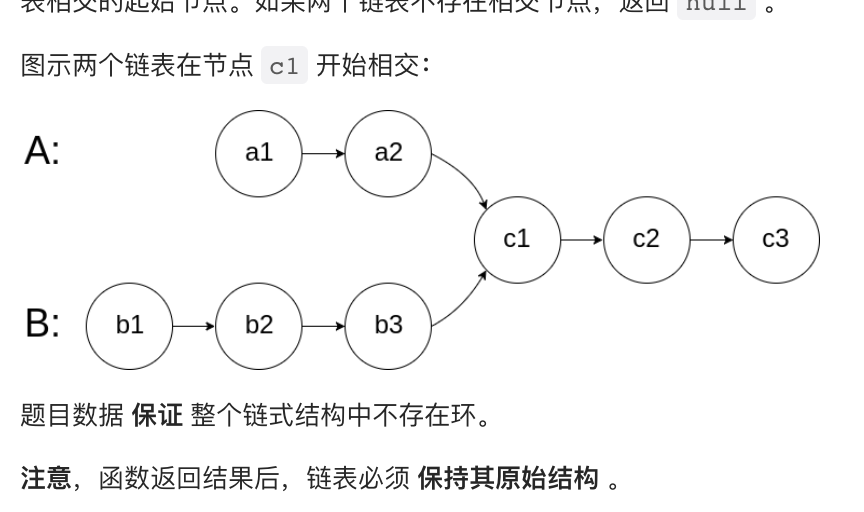

这个也很简单，只要两个同步的指针，每个指针分别遍历A和B即可，当他们指向同一个节点，那么就证明相交，如果最种指向nullptr，则说明不相交。这个原理很简单，因为他们的总路程相等，那么最终他们一定会走到相交点上，然后走完共同的路。

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* p1 = headA;
        ListNode* p2 = headB;
        while (p1 != p2) {
            if (p1 == nullptr) {
                p1 = headB;
            } else {
                p1 = p1->next;
            }
            if (p2 == nullptr) {
                p2 = headA;
            } else {
                p2 = p2->next;
            }
        }
        return p1;
    }
};

总结

双指针算法，一般采用的是一个快一个慢，两个配合起来达到目的。这种算法属于见过了就会知道，没见到过就会很麻搭。对于链表的问题，多画图会起到更好的效果。