最小树算法

发表于 | 分类于 | |
字数统计: 1,390 | 阅读时长 ≈ 6

什么是最小生成树

在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集且为无循环图，使得联通所有结点的的 w(T) 最小，则此 T 为 G 的最小生成树。

说人话就是：最小生成树一般是指在一个连通图内，如何生成一颗树，使得各个节点都是树的节点，且相加的权重最短。

最小树算法一般有两种算法，一个为Kruskal算法， 另一个为Prim算法。

最小生成树的应用场景

生成树和最小生成树有许多重要的应用，例如要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

Kruskal算法

这个算法相当容易理解，首先把图的所有顶点看做是只有根的树，然后合并树，合并的原则是选取最小的权重的边，且不能是树形成圈。如下图所示：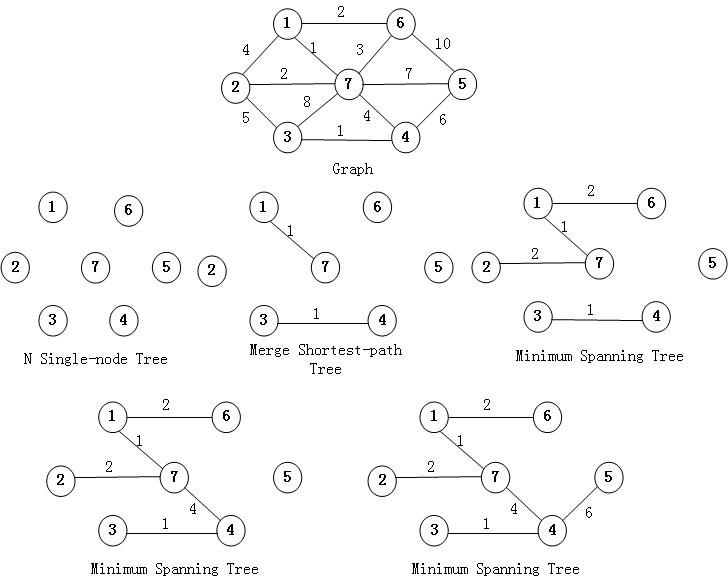

这个朴素的算法和我们的并查集好像啊。回想一下，我们的并查集就是这样做的啊。

具体的做法如下：

  • 我们首先将各个权重边排序。
  • 选择最小的权重边，将边的两个顶点连接到一起，这时要判断如果形成了环，说明非法，因此不能合并。如果可以合并，则合并，并记录权重值的和。
  • 递归上一步的操作，直到遍历完所有的边为止。

前文也说道过，图一般用邻接表或者邻接矩阵来表示，我们要通过图生成最小生成树，就要把数据结构先做下转换了，我们需要以边为中心来构造数据结构

1
vector<vector<int>> edges;

对于edge[0],edge[1]表示边的两个顶点，edge[2]表示边的权重。

那么我们就可以有如下的模板代码

  • 主要代码为buildMST，首先排序，然后看合并是否会成环，如果不会，则merge，会则继续下个权重边的点merge
  • Union/Find/IsCycle这些都是并查集的基本功能。因此Kruskal算法的本质就是并查集。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
vector<int> parents;

void Union(int p, int q)
{
    int fatherP = Find(p);
    int fatherQ = Find(q);
    parents[fatherP] = fatherQ; 
}

int Find(int node)
{
    while (parents[node] != node) {
        parents[node] = parents[parents[node]];
        node = parents[node];
    }
    return parents[node];
}

bool IsCycle(int p, int q)
{
    int fatherP = Find(p);
    int fatherQ = Find(q);
    if (fatherP == fatherQ) {
        return false;
    }
    return true;
}

int buildMST(int numsPoint, vector<vector<int>> edges)
{
    parents.resize(numsPoint);
    for (int i = 0; i < numsPoint; i++) {
        parents[i] = i;
    }
    sort(edges.begin(), edges.end(), [](vector<int> a, vector<int> b) -> int { return a[2] - b[2]; });
    int minWeight = 0;
    for (auto& edge : edges) {
        if (!IsCycle(edge[0], edge[1])) {
            Union(edge[0], edge[1]);
            minWeight += edge[2];     
        }
    }
    return minWeight;
}

Prim算法

Kruskal算法是以边为中心构建树，而Prim算法则是以点为中心来构建树。
下面我们来分析下Prim算法。

  • 我们可以随机选择一个点V1，那么最终的树肯定要包含与v1点联通的3个边之一，那么我们就选最小的。
  • 这样我们的集合中就有了两个点v1和v7，然后我们在v1和v7的所有边中，再选择一个最小的边，这样我们就又了三个点v1，v7，v2
  • 递归上面的选择，因为我们每次在现有的选择中选择了最小的边，因此最终生成的树叶一定是权重最小的树

下面我们归纳下Prim的模板实现

  • 首先定义数据结构，Kruskal算法是以边为中心，而Prim是以点为中心，因此定义的图的数据结构也是不同的

    1
    2
    3
    4
    vector<vector<vector<int>>> graphs;
    graphs[0]表示点0对应的边信息
    graphs[0][0]表示点0对应的第一条边的信息
    graphs[0][0]包含三个元素，分别为启示点，终点，以及权重。

  • 其次每次需要取最小权重的边，这就是priority_queue。因此在BFS中应用priority_queue存放信息

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Comp{
    public:
    bool operator()(vector<int>& a, vector<int>& b){
        return a[2] - b[2];
    }
};

priority_queue<vector<int>, vector<vector<int>>, Comp> pq;

vector<bool> inMST;

int minWeight = 0;
 
void SelectNext(int index, vector<vector<vector<int>>>& graphs)
{
    for (auto& edge : graphs[index]) {
        int to = edge[1];
        if (inMST[to]) { // 如果这个点已经在树中了，那么就不能再加这条边了，否则会成环
            continue;
        }
        pq.emplace(edge);
    }
}
void buildMSTPrim(vector<vector<vector<int>>>& graphs)
{
    int numsPoint = graphs.size();
    inMST.resize(numsPoint, false);

    // 选择第0个点开始遍历
    inMST[0] = true;
    SelectNext(0, graphs);
    while (!pq.empty()) {
        auto edge = pq.top();
        pq.pop();
        int to = edge[1];
        int weight = edge[2];
        if (inMST[to]) {
            continue;
        }
        minWeight += weight;
        inMST[to] = true;
        SelectNext(to, graphs);
    }
}

1584. 连接所有点的最小费用

下面分别用Prim算法和Kruskal算法来处理下这个问题

总结

Prim算法和Kruskal算法，本质上讲都是利用的贪心算法。只不过一个以点为切入点，一个以边为切入点。

显示 Gitment 评论