思考一个问题,空间是什么?我们现实中是3维空间,我们将整个空间抽象出来,那么每个人都是空间中的一个点,那么只要定义好一个坐标系,那么每个人的位置都可以对应着具体的坐标。实际上物理学我们也知道,空间是可以用坐标系来定义的。
那么从一个空间变化到另一个空间怎么做呢?实际上就是从一个空间坐标系的表示变换为另一个空间坐标系的表示,学习过矩阵论,那么我们就可以很清晰的知道,我们只需要乘以一个变换矩阵就可以了。
回顾一下一个点在空间中的变换,无外乎是缩放,旋转和位移。
我们在空间中的坐标可以表示为一个由原点指向坐标点的向量。当我们对这个向量进行缩放时,实际上的效果并不一定是一个等比例的,如图所示: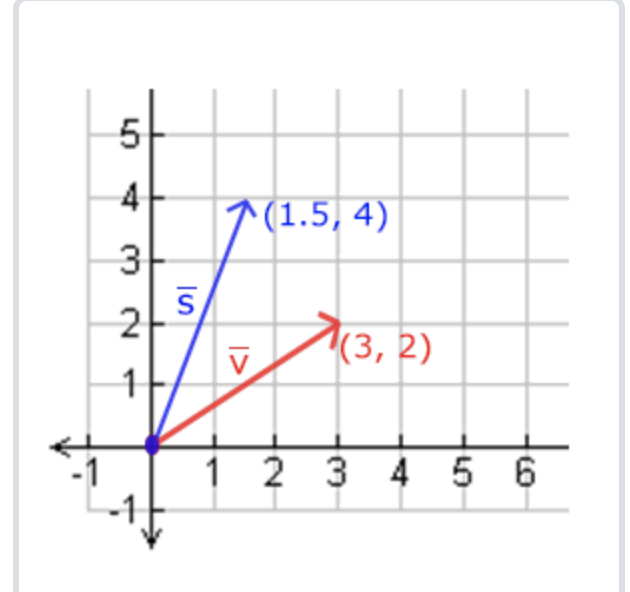
向量的缩放可以对每个坐标分量进行分别缩放,用矩阵表示,则如下所示: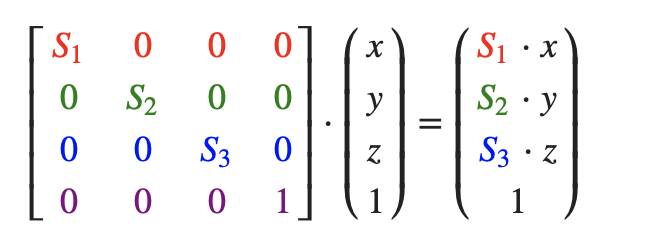
平移:
平移的操作也是比较简单,实际上就是给每个分量加上一个平移量,矩阵变换如下所示:
旋转:
定义旋转,一般需要两个物理量,一个是旋转轴,一个是旋转的角度(弧度),如下图所示: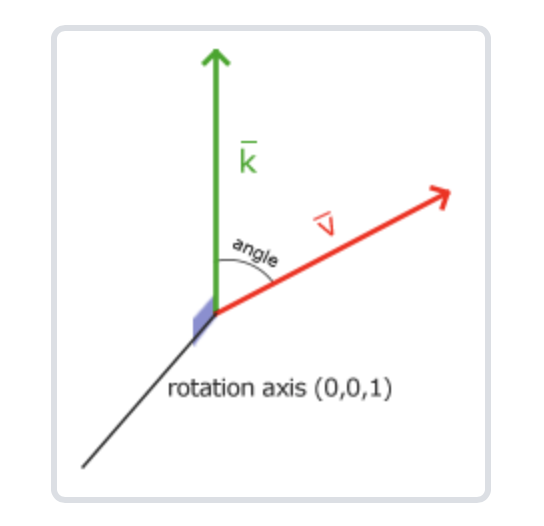
沿着坐标轴的转换公式如下:
而沿着任意轴(Rx,Ry,Rz)旋转的公式如下所示:
好复杂,而在实际应用中,我们一般都是用四元数,通过调用一些库函数可以直接计算得到我们的旋转矩阵。
glm库1
2glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
上面表示构造一个位移的矩阵,将物体的位置移动(1.0,1.0,0.0)个单位1
2
3glm::mat4 trans;
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));
上面表示构造一个旋转以及缩放的矩阵,表示将物体逆时针旋转90度,然后缩放为原来的0.5倍
这样通过上面的内容,我们就能够把空间的变换用矩阵的形式来解决了。
参考资料:
https://learnopengl-cn.github.io/01%20Getting%20started/07%20Transformations/#glm