空间变换
在计算机图形学中,我们将一个物体渲染到最终的屏幕上是需要经过一系列的空间变化的,如下图所示: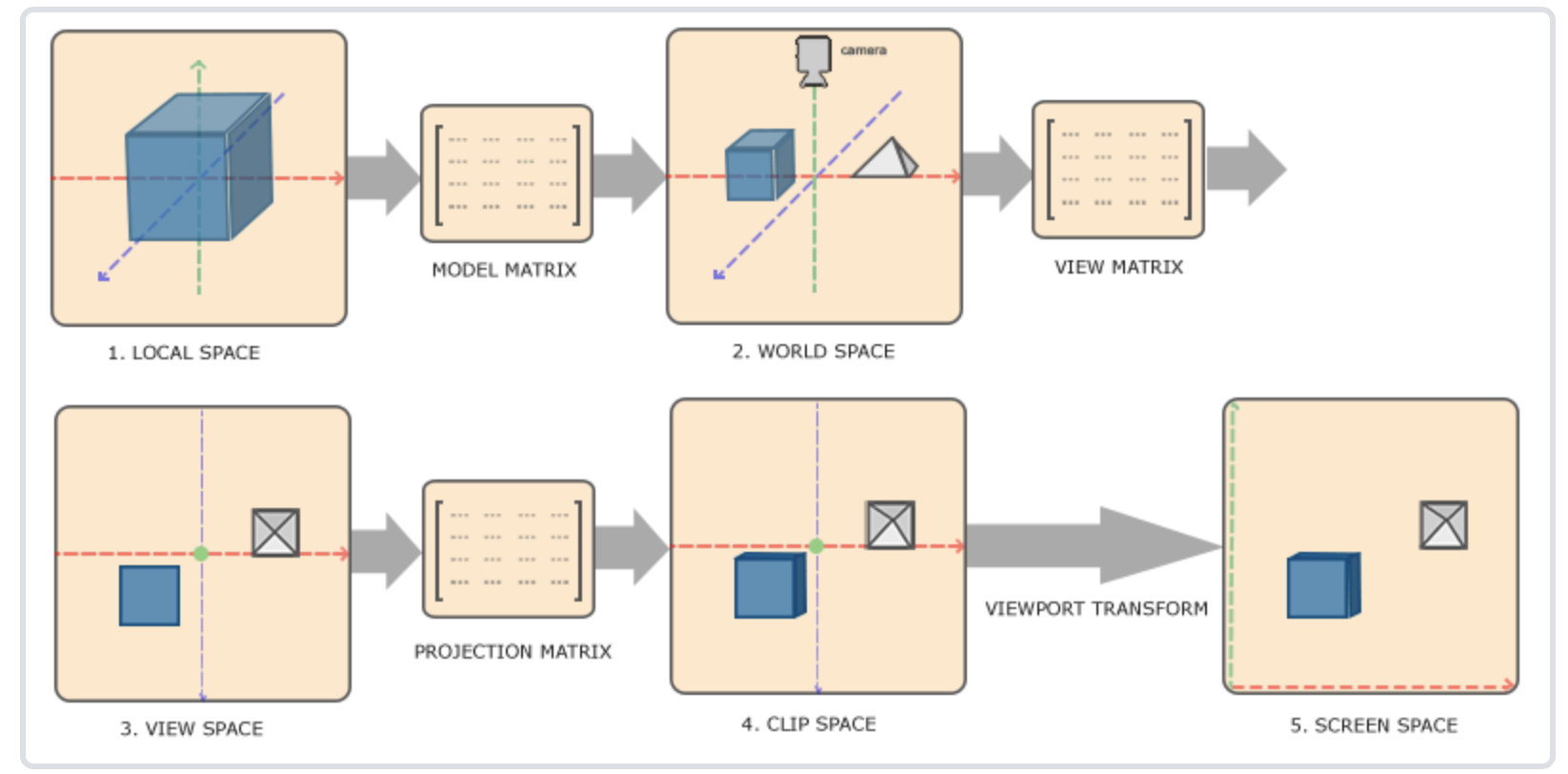
我们可以看到M矩阵是将物体从局部空间变换到世界空间,V矩阵是将物体从世界空间变换到观察空间。本章节我们重点看下P矩阵,它将物体从观察空间变换到裁剪空间。为什么要做这个变化呢?在上图中我们的view space和clip space看起来是一样的啊。
为什么要做投影变换
投影变换的一个最主要的原因是要将物体从view space变换到NDC(Normalized Device Coordinates)坐标系中。NDC坐标系是指在x/y/z的值在[-1, 1]之间的坐标系。实际上可以理解其为一个立方体。而我们通过投影变换将物体从观察空间变换到裁剪空间。实际上就是将摄像机能看到的物体变换到NDC空间上,那么下步就可以在显示到屏幕上了。
投影变换有两种,分别对应着理想情况下的正交投影和实际现象的透视投影两种
正射投影
正射投影也就意味着对于摄像机而言,物体的远近大小是一样的,虽然这不符合实际,但是这个在有些场景下还是需要使用的(比如阴影等)
我们知道将一个物体从一个空间变换到另一个空间,需要做的就是乘以一个变换矩阵。对于正射投影,我们要做的就是把视锥内的物体变换到一个正方体中(NDC)。如下图所示:
下面我们来推导下正射投影的矩阵:
假设我们的视锥(物体在视锥内)为左上角的长方体,那么我们要做的就是将其平移到中心点,然后再将其缩放为正方体,那么这个矩阵就好写了,就是一个平移外加一个缩放,如下所示:
对于我们大部分场景来说,我们的场景视锥应该是对称的,也就是变换后的NDC的原点也应该再我们的视锥的对称面上,因此有
$r=-l$和$t=-b$,但是$n\neq-f$,因此正射投影的矩阵可以写为:
其中$w,h,n,f$分别表示视锥的宽,高,相机的近,远平面。
注意:这里推导出来的公式可能跟某些地方的不太一致,这是因为对z的定义导致的。如果我们认为近远平面的范围是[-1,1], 那么就是上面的公式,如果我们设定近远平面的范围是[0, 1],那么公式就应当为如下所示:
同时对于左手坐标系,上面的公式也是有些许的变化的
透视投影
正射投影比较简单,一个平移一个缩放,顺序无所谓,主要是没有产生形变,所以可以这样简单的变换。但是透视投影可不一样了,透视投影也就意味着近处的物体大,远处的物体小,并且在无穷远处交于一点。因此透视投影的推导会相对有一些难度。
透视投影:
对于透视投影我们要做的是什么?就是把左边的这个视锥空间转换为右边的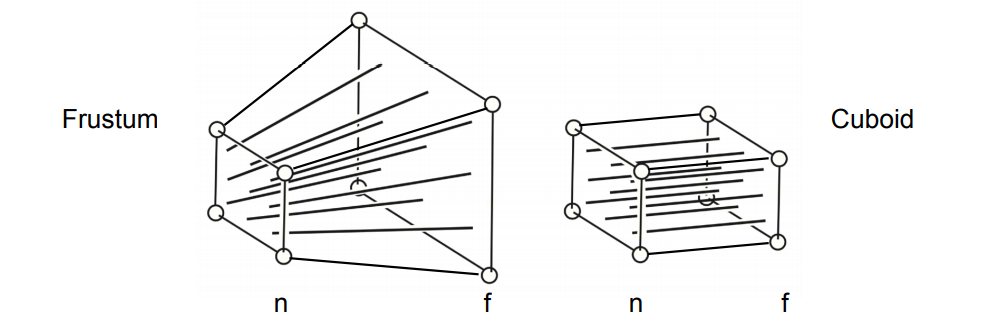
下面我们要引入相机的一些知识了。
对于相机而言,它有一个近平面,有一个远平面, 也就是说只有在这两个平面之间的物体才能被相机看到。它还有一个视角,实际上就是两个平面连线相交形成的角度。

而对于透视视锥,有如下的相似三角形原理
有了这些参数,以及上面的基础知识,我们就可以推导透视投影矩阵了。
我们还是看下面的这张图:

我们先将视锥体变换为近平面大小的长方体
对于边界上线段上的点,根据相似三角形原理,我们可以得到如下的结论:
点$(x^{‘}, y^{‘}, z^{‘})$ 要变换成与近平面平行的点(x, y相同,z不同),根据相似三角形原理,有如下的变换:
对于齐次坐标,有如下的公式:
因为有如下的变换等式:
因次我们可以得到M矩阵的部分值,第三行未知。
但是第三行一定是$(0, 0, A, B)$的形式,这是因为近平面左上角的点,乘以M矩阵是不变的,如下所示:
因此,我们得到了如下的等式:
同时不要忘记了我们还有远平面,对于远平面上的点,投影前后它的z值是不变的,因此有:
也就有如下的方程:
可以解出:
$A = n + f$
$B = - n*f$
因此我们已经有了$M_{persp \Rightarrow ortho}$矩阵,如下所示:
有了矩阵后,我们可以将视锥变换到正射投影空间,我们只需要再乘以矩阵就可以将其变换到NDC空间了。因此我们的透视投影的推导可以分成两部分,先将其变换到ortho空间,然后再利用矩阵将其变换到NDC空间即可。
因此有:
对于透视投影的相机,一般有如下的参数:
$fov$ :视角 $tan(\frac{fov}{2}) = \frac{h}{n}$
$aspect$ : 宽高比 $aspect = \frac{w}{h}$
$far$ :远平面 $f$
$aspect$ : 近平面 $n$

因此上面的公式可以简化为:
为什么不同的地方看到的公式不太一样
这是因为左右手坐标系不同导致的,同时我们的z的范围是[-1, 1]还是[0, 1],这也会导致最终的矩阵有差异。可以参见glm的实现。
在glm中根据是左右手坐标系以及[-1, 1]还是[0, 1],分了四种场景,如下所示:1
2
3
4
5
6
7
8
9
10
11
12
13template<typename T>
GLM_FUNC_QUALIFIER mat<4, 4, T, defaultp> ortho(T left, T right, T bottom, T top, T zNear, T zFar)
{
# if GLM_COORDINATE_SYSTEM == GLM_LEFT_HANDED && GLM_DEPTH_CLIP_SPACE == GLM_DEPTH_ZERO_TO_ONE
return orthoLH_ZO(left, right, bottom, top, zNear, zFar);
# elif GLM_COORDINATE_SYSTEM == GLM_LEFT_HANDED && GLM_DEPTH_CLIP_SPACE == GLM_DEPTH_NEGATIVE_ONE_TO_ONE
return orthoLH_NO(left, right, bottom, top, zNear, zFar);
# elif GLM_COORDINATE_SYSTEM == GLM_RIGHT_HANDED && GLM_DEPTH_CLIP_SPACE == GLM_DEPTH_ZERO_TO_ONE
return orthoRH_ZO(left, right, bottom, top, zNear, zFar);
# elif GLM_COORDINATE_SYSTEM == GLM_RIGHT_HANDED && GLM_DEPTH_CLIP_SPACE == GLM_DEPTH_NEGATIVE_ONE_TO_ONE
return orthoRH_NO(left, right, bottom, top, zNear, zFar);
# endif
}
关于左右手坐标系
下图所示就是左右手坐标系的差异,我们可以看到实际上就是z的朝向的问题,这也就意味着不同的坐标系,near和far的大小是不同的,这也就意味着我们的公式也是不同的。
openGL一般是左手坐标系,而vulkan是右手坐标系。