算法思想
Floyd算法是一个可以处理有向图或负权重的最短路径问题的一个算法。她的算法思想很简单,就是:
如果想要让任意两个点间的距离缩短,那么必然要引入第三个点,只有通过第三个点的中转,才能实现缩短路程。
假设为到的只以集合中的节点为中间节点的最短路径的长度,那么如果最短路径经过点,则:
如果最短路径不经过点$k$,则:
因此:
距离实例解析:
请参见下面的案例:
5行代码的实现
1 | for(k=1;k<=n;k++) |
已案例中的例子分析一下这段代码:
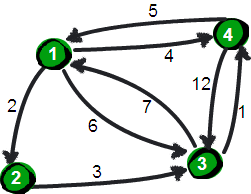
当时,if之前,为到的直达,或到经过点1的距离的最小值
所以$k=2$时,整个函数是到经过2的的距离或到的直达,或到经过1,2的距离的最小值。
Floyd是多源路径算法,能够求得任意两点之间的距离。就是效率比较差,时间复杂度为,空间复杂度为。