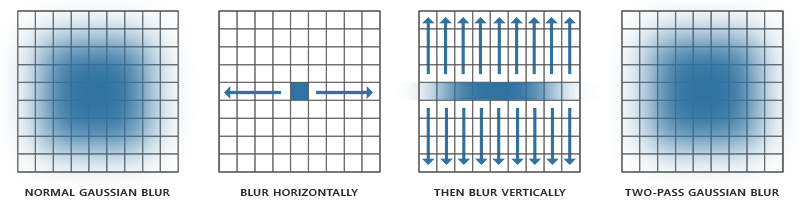
图像的模糊是一个很常见的内容,现实中有很多的算法,比如平均值模糊啊等等。但是对于图像而言,一个点的值受它周围的点的影响的权重值是不同的,距离越近,权重越大,因此平均值模糊明显是不合适的。对于这种场景,高斯模糊天然符合。
1)高斯函数
下面的是一维的高斯函数,我们可以看到对于中间点,他的周围的点的权重随着距离的增加而降低,这是非常符合我们的需求的
而我们的图像是二位数据,因此下面的二维高斯函数才是我们这里需要使用的。
二维高斯函数的方式如下: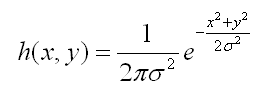
2)如何做高斯模糊
假设我们要对一个点做3*3的高斯模糊,首先我们定义当前点的坐标为(0,0),其他店的坐标如下所示:
当我们定义sigma=1.5,那么将坐标输入到上面的方程中,可以得到:
这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵: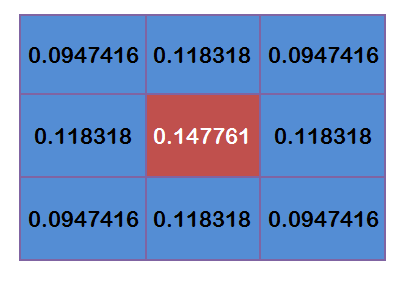
下面我们来计算高斯模糊:
假设这9个点的像素值为:
乘以上面的高斯矩阵,可得到: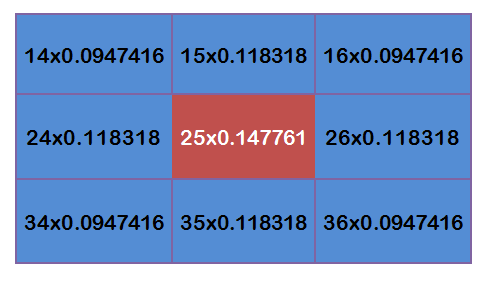
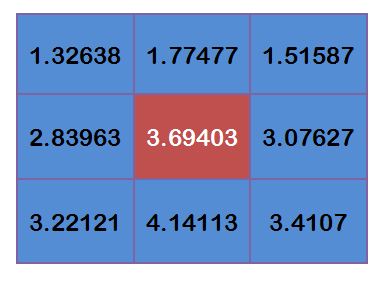
将这9个值加起来,就是中间点的高斯模糊的值。重复这个过程,就可以得到整个图像的高斯模糊的结果了。
3)图像的边界怎么处理
一个变通方法,就是把已有的点拷贝到另一面的对应位置,模拟出完整的矩阵。
4)优化
上面的做法很简单,但是有一个问题,我们对一个点做高斯模糊,那么我们要用到周围的多少个点?9个。这也没啥,但是当我们的卷积核是3232的呢,那么就意味着每个点做高斯模糊,我们要采样周围的3232=1024个点,这个计算量可是不小的。那么怎么办呢?
幸运的是,高斯方程有个非常巧妙的特性,它允许我们把二维方程分解为两个更小的方程:一个描述水平权重,另一个描述垂直权重。我们首先用水平权重在整个纹理上进行水平模糊,然后在经改变的纹理上进行垂直模糊。利用这个特性,结果是一样的,但是可以节省难以置信的性能,因为我们现在只需做32+32次采样,不再是1024了!这叫做两步高斯模糊。