KernelPCA

算法思想

之前的博文里面介绍了PCA算法，作为一个经典的基于线性代数的降维方法，PCA算法对线性数据效果良好。然而如果我们的数据是非线性的（这才是社会的现实啊），那么PCA算法就呵呵了。
那么对于非线性问题怎么处理呢？上一章我们讲解了kernel的思想，核就是为了解决非线性问题而诞生的，其将非线性数据映射为高维的线性数据，这样就可以应用PCA了。因此将kernel引入到PCA的算法中，就诞生了KernelPCA算法

回忆PCA

假设原始数据为$X_{m*n}$， m为样本个数，n为特征个数，其对应的协方差矩阵为C，P为基变换矩阵，那么有：

$$Y = XP$$

Y为变换后的矩阵，其协方差矩阵为D，那么我们的目的就是变换后的矩阵的协方差矩阵的主对角线的值最大化，其他值为0。因此有：

$$D = \frac{1}{m}Y^TY = \frac{1}{m}(P^TX^T)(PX) = P^T(\frac{1}{m} X^TX )P = PCP^T$$

因此转换矩阵P就是能让原数据的协方差矩阵对角化的矩阵。

而P矩阵按特征值的大小排列的前k行主成的矩阵$X$ 乘以矩阵$P_k$就是X从n维降到k维的变换，$XP_k$就是前k个主成分组成的矩阵。

本质上讲PCA就是将协方差矩阵$X^TX$对角化。

引入kernel到PCA

我们回想下核就是将低维数据的内积对应的高维数据的内积用核函数表示，这里正好有内积$X^TX$，假设我们的映射函数为$\phi(X)$,那么对于非线性数据，我们可以直接对高维的$\phi(X)^T \phi(X)$做特征值分解就可以了啊。

下面是错误的推导

根据PCA的原理，我们可以定义核矩阵$K = \phi(X)^T \phi(X)$

因此有：

$$K \alpha= \lambda \alpha$$

对K做特征值分解得到特征向量矩阵P，用P乘以映射到高位的数据$\phi(X)$就可以得到降维后的数据$Y = \phi(X)P$

能这样计算么？首先两个问题，

1. 对于核映射，我们不知道映射函数的表达式具体是什么，这也就导致上面的式子根本无法计算
2. 还有一个问题，我们定义的$K \alpha= \lambda \alpha$是核么？不是。

核函数矩阵为$K = \phi(X) \phi(X)^T$，而不是上面的形式。

PCA中的协方差矩阵是特征的内积，而核函数是样本的内积，这是不同的

因此上面的理解是错误的，下面我们推导一下。

核PCA的推导

假设$W$是高维空间的映射基，则有：

$$\phi(X)^T \phi(X) W = \lambda W$$

可得有：

$$W = -\frac{1}{\lambda} \phi(X)^T \phi(X) W = \phi(X)^T \alpha$$

其中：

$$\alpha = -\frac{1}{\lambda} \phi(X) W$$

将$W = \phi(X)^T \alpha$带入到$\phi(X)^T \phi(X) W = \lambda W$中有：

$$\phi(X) \phi(X)^T \phi(X) \phi(X)^T \alpha = \phi(X) \lambda \phi(X)^T \alpha$$

因为核矩阵$K = \phi(X) \phi(X)^T$，所以有：

$$K^2 \alpha = \lambda K \alpha$$

两边删除$K$，有：

$$K \alpha = \lambda \alpha$$

对核特征矩阵$K$做特征值分解，得到特征向量矩阵$A$

给定新的数据$X_{new}$,则其在高维空间的降维映射为：

$$\phi(X_{new}) W = \phi(X_{new}) \phi(X)^T \alpha = K(X_{new},X)A$$

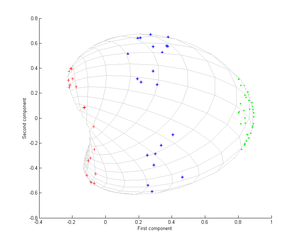
KernelPCA的效果

PCA只是对原始数据做了旋转操作

而KernelPCA对原始数据投影到了线性可分的场景

下图就是线性PCA的效果：

这个是多项式核的结果：

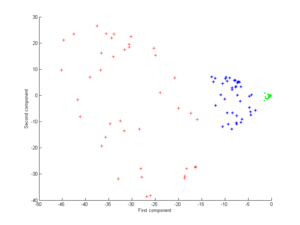
这个是高斯核的结果：