流行是什么

manifold就是局部具有欧氏空间性质的空间。在manifold上足够小的区域近似于欧几里得空间。具体说明我们的地球就是一个manifold。当我们在地面上，我们认为地球是平的，两点间的距离可以直接用欧氏距离直接计算，这个也不会引入太大的误差，而站在地球的角度上看，两点的距离这样算是不对的，但是who care，只要局部能够近似为欧氏空间就行。（这句话说得专业一点就是：流行在局部上与欧式空间同胚）

等度量映射

低维流行嵌入到高维空间后，直接在高维计算直线距离有误差，因为高维中的直线在低维嵌入流行上是不可达的。这就是等距离度量的一个基础，如下图所示：

Kernel_pca

作图上的两个点的欧氏距离不等于她的实际距离，想象一只蚂蚁从一点爬到另一点，只能走红线，而不能走黑线，因此在高维空间中，红线的长度才是真实的距离。

那么怎么度量这个距离呢？这就利用到了流行的定义：流行在局部上与欧式空间同胚。也就是在局部可以用欧氏距离计算，然后一步步的累加得到真实距离。

因此我们可以为每个点寻找临近点，建立近邻连接图，计算两点之间的测地线距离就变为了计算近邻图上两点间的最短路径问题。

因此我们的高维流行就转换为了图的问题。

对于图的最短路径问题，我们有很多算法，比如说深度优先与广度优先，Dijkstra算法以及Floyd算法等等。

当我们得到了具体模型后，我们可以直接用MDS算法得到低维的坐标，也就实现了降维的功能。

局部线性嵌入（LLE）

其实无论哪种降维方法，都是有一些要保留一些基本原则的，比如说PCA，保留信息量，MDS保留样本距离不变等等。

那么LLE的基本思想就是保持邻域内样本间的线性关系。即：

$x_i = w_{ij}x_j + w_{ik}x_k + ... + w_{il}x_l$

LLE希望上式在低维空间空能够保持。

LLE

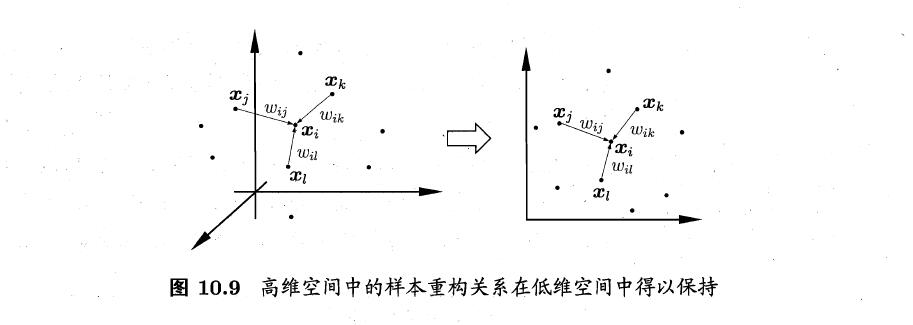
LLE首先为每个样本 $x_i$ 找到其近邻样本的下标集合 $Q_i$ ，计算基于 $Q_i$ 中的样本点对 $x_i$ 进行重构的系数。即：

$min_{w_1,...,w_m} \sum_{i=1}^{m}||x_i - \sum_{j \in Q_i} w_{ij}x_j||^2_2$ $s.t. \sum_{j \in Q_i} w_{ij}=1$

由拉格朗日乘子法，有：

$w_{ij} = \frac{\sum_{k \in Q_i} C_{jk}^{-1}}{\sum_{l,s \in Q_i} C_{ls}^{-1}}$

其中：

$C_{jk} = (x_i - x_j)^T(x_i - x_k)$

根据LLE的基本假设：在低维空间中保持线性关系不变，即 $w_i$ 不变，有：

$min_{z_1,...,z_m} \sum_{i=1}^{m}||z_i - \sum_{j \in Q_i} w_{ij}z_j||^2_2$

这个式子的优化目标变为给定 $w_i$ ，优化 $z_i$ ， $z_i$ 是 $x_i$ 在低维空间的坐标。

令：

$Z = (z_1,z_2,..,z_m) \in R^{d'*m}$ $(W)_{ij} = w_{ij}$

令:

$M=(I - W)^T(I - W)$

则优化的式子可以写为：

$min_{Z} tr(ZMZ^T)$ $s.t. ZZ^T = I$

理解一下上面的优化条件：如果将 $M$ 对角化，那么 $tr(ZMZ^T)$ 就是特征值的和。因此对 $M$ 做特征值分解， $M$ 的 $d'$ 个最小的特征值对应的特征向量组成的矩阵即为 $Z^T$ 。

总结

其实基于流行的降维算法本质上就用到了一点：流行在局部上与欧式空间同胚。记住这个很重要。